The basic requirement from an energy function is, that the free energy of native complex will be lower  than that of any misdocked geometry, for the same pair of proteins. Thus misdocked complexes show how the energy function should not look like. This information can be extracted in the form of constraints (inequalities) on the energy function:

  Optimization of linear energy functions

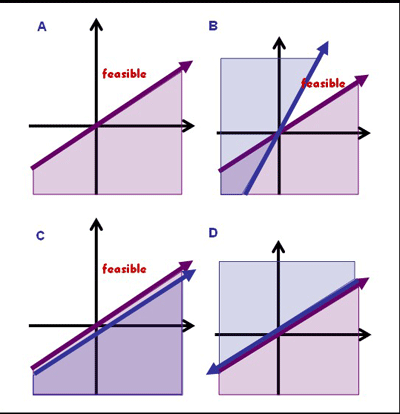
The choice of a linear form for the energy function enables us to efficiently optimize the parameters, such that, the energy of the native state will be lower than that of every non native state. Each inequality divides the parameter space into two regions,  accessible (each point in the space represent a valid solution) and inaccessible.  A given inequality may give rise to three outcomes: It may (i) reduce the space allowed for the parameter set (most desirable), (ii) have no effect on the allowed space or (iii)  impose an impossible condition (no solution exists) (D). Optimization in our study was performed using the interior point algorithm BPMPD

Ref: "Optimal Design of Protein Docking Potentials: Efficiency and Limitations"Dror Tobi & Ivet Bahar. Proteins: Structure, Function, and Bioinformatics 62, 970-981, 2006 .